# 数据类型
# 值类型
- let a;//underfind (const 的定义的常量必须有初始值)
- const a = '' //string
- const a= 1 //number
- const a = true //boolean
- const a = Symbal('s')
# 引用类型
为什么设计引用类型?
性能和存储的问题,值类型占用空间小,可以存在栈中。
引用类型数据大,存在栈中不好管理。如果复制栈中的对象会很慢。
- 数组
- 对象
- null
let a = 100
let b = a
a =200
console.log(b) // 100
值在栈中存储。

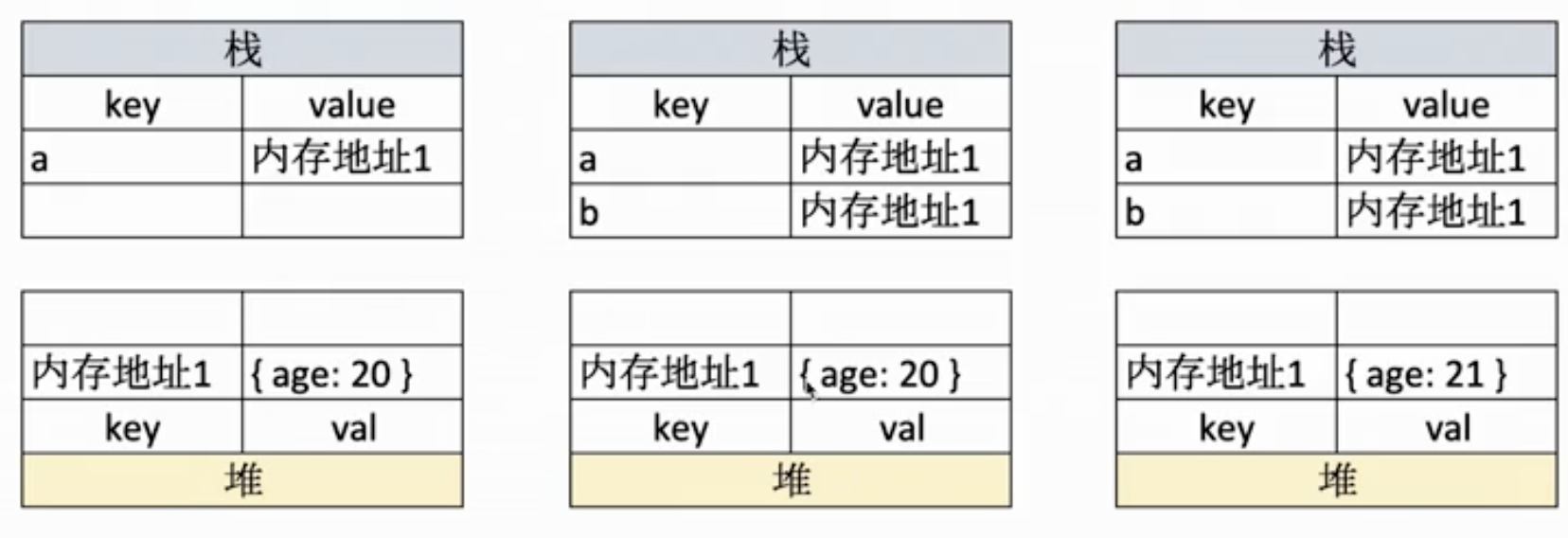
let a = {age:20}
let b = a
a.age = 21
console.log(b) // {age:21}
引用类型,变量在栈中存储,对应的值存储的是引用地址,引用的值存储在堆中。
值在栈中存储。
深拷贝和浅拷贝都是针对的引用类型,JS 的变量类型分为值类型和引用类型; 值类型:存在栈中,对值类型拷贝会对值进行复制。 引用类型:会进行地址的拷贝,最终两个变量会指向同一个地址。
// 引用类型指向同一份数据,会导致a b指向同一份数据,此时如果对其中一个进行修改,就会影响到另外一个
var a = {c: 1};
var b = a;
a.c = 2;
console.log(a.c, b.c); // 2, 2 全是2,a b指向同一份数据
# 深拷贝 VS 浅拷贝
深拷贝和浅拷贝都是针对引用类型来的,
- 浅拷贝只拷贝一层数据。
- 深拷贝递归遍历对象。
var a1 = {b: {c: {}};
var a2 = shallowClone(a1); // 浅拷贝
a2.b.c === a1.b.c // true
var a3 = clone(a1); // 深拷贝
a3.b.c === a1.b.c // false
简版深拷贝实现(递归)
function deepClone(json = {}) {
if(typeof json !== 'object'||json == null){
return json;
}
let result;
if(json instanceof Array){
result = []
}else{
result = {}
}
for(let key in json){
//保证key是json自身的属性
if(json.hasOwnProperty(key)){
result[key] = deepClone(json[key])
}
}
return result;
}
深拷贝(序列化反序列化实现)
- JSON.parse(JSON.stringify(test))
- Date 类型转换回来之后 Date 会变成字符串
- 转换的对象中有函数,undefined,则序列化的结果会把函数或 undefined 丢失;
- 有 NaN、Infinity 和-Infinity,则序列化的结果会变成 null
var test = {
name: 'a',
date: new Date,
};
//{name: "a", date: Tue Aug 03 2021 11:33:33 GMT+0800 (中国标准时间)}
console.log(JSON.parse(JSON.stringify(test)))
//{name: "a", date: "2021-08-03T03:33:33.101Z"}
(原因:string 转 obj 时候,undefined、function、symbol 会在转换过程中被忽略。。。)
const test = {
a: null,
b: function() {
console.log('fff')
},
c: underfund
};
// {a: null, c: undefined, b: ƒ}
// {}
console.log(JSON.parse(JSON.stringify(test)))
# 浅拷贝实现
function shallowClone(source) {
var target = {};
for(var i in source) {
if (source.hasOwnProperty(i)) {
target[i] = source[i];
}
}
return target;
}
# 判断引式类型
Object.prototype.toString.call()
Object.prototype.toString.call(undefined) //[object Undefind]
Object.prototype.toString.call(new Error('111')) //[object Error]
Object.prototype.toString.call(arguments) // [object Arguments]
Object.prototype.toString.call(null) //[object Null]
Object.prototype.toString.call([]) //[object Array]
Object.prototype.toString.call({}) //[object Object]
Object.prototype.toString.call(function(){}) //[object Function]
Array.isArray
obj instanceof Object
# typeof 运算符
可以判断的类型 可以识别所有值类型
underfind
string
number
boolean
symbal
判断函数
typeof funcation a(){} // function
# instanceof 实现
寻找左边的对象的原型链中是否存在右边对象的原型对象。
function instanceof(left,right) {
let l = left.__proto__;
let r = right.prototype;
while (true){
if(l === null){
return false;
}
if(l === r){
return true;
}
l = r.__proto__;
}
}
# 类型转换
强制类型转换比如:parseInt parseFloat toString
隐式类型转换:
- 1 if判断
- 2 逻辑运算
- 3 ==判断
- 4 字符串拼接等
比如: 12 + '10' //输出结果 1210 (先把12转为string,在进行字符串拼接)
console.log(undefined==null) //true
console.log('0'==0) //true 字符串转数字
console.log(0==false) //true 布尔转数字
console.log('0'==false) //2个都转成数字
console.log(null==false) //false
console.log(undefined==false)//false
# 判断两个对象相等
function equal(a, b) { ... }
判断两个NaN相等?
isNaN() 来判断一个值是否是数字。原因是 NaN 与所有值都不相等,包括它自己。
// 主要利用NaN永远不等于自身
let a,b = NaN;
console.log(a == b);//false
function equal(a, b) {
return a !== a && b !== b;
}
console.log(equal(NaN, NaN)); // true
区分0和-0?
JavaScript 采用了IEEE_754 浮点数表示法,1000(-0) 和 0000(0)都是表示 0 ,这才有了正负零的区别。
-0.1.toFixed(0) === -0
Math.round(-0.1) === -0
(-0).toString() // '0'
(+0).toString() // '0'
0 === -0 // true
function equal (a,b){
//返回的是正负无穷 Infinity 或者 -Infinity
return a === b && 1/a === 1/b
}
let a = { a: {age:25}, b: 2, c: {}}
let b = { c: 3, a: { name: 'kira' },f: {} };
function isObject(target){
return (typeof target === 'object' && target !== null) ? true : false
}
function merge(target,source){
let result;
if(isObject(source)){
Array.isArray(source) ? result = [] :result = {};
for (let key in source){
if(isObject(source[key])){
merge(target[key],source[key]);
}
result[key] = source[key]
}
return result;
}
}
merge(a,b)
# 精度问题
js中整数和小数只有一种数字类型:Number,它的实现遵循IEEE 754标准,使用64位固定长度来表示,也就是标准的double双精度浮点数。在二进制科学表示法中,双精度浮点数的小数部分最多只能保留52位,再加上前面的1,其实就是保留53位有效数字,剩余的需要舍去,遵从“0舍1入”的原则。
0.1 + 0.2 !== 0.3
浮点数转二进制的过程如下
- 整数部分采用 /2 取余法
3 => 3/2 = 1 余 1
1 => 1/2 = 0 余 1
所以 3(十进制)= 11(二进制)
4 => 4%2 = 2 余 0
2 => 2%2 = 1 余 0
1 => 1%2 = 0 余 1
所以 4(十进制)= 100(二进制)
- 小数部分采用 *2 取整法
0.5 => 0.5*2 = 1 取整 1
0.5(十进制)= 0.1(二进制)
0.1 => 0.1*2 = 0.2 取整 0
0.2 => 0.2*2 = 0.4 取整 0
0.4 => 0.4*2 = 0.8 取整 0
0.8 => 0.8*2 = 1.6 取整 1
0.6 => 0.6*2 = 1.2 取整 1
0.2 => 0.2*2 = 0.4 取整 0
0.4 => 0.4*2 = 0.8 取整 0
0.8 => 0.8*2 = 1.6 取整 1
0.6 => 0.6*2 = 1.2 取整 1
...发生循环
得到结果 0.1(十进制)= 00011001100110011001100110011... (0011)循环(二进制)
0.1 转二进制会发生无限循环,而 IEEE 754 标准中的尾数位只能保存 52 位 有效数字,所以 0.1 转二进制就会发生舍入,所以就产生了误差。
解决方法:
- 使用 JavaScript 提供的最小精度值判断误差是否在该值范围内 Math.abs(0.1 + 0.2 - 0.3) <= Number.EPSILON
- 转为整数计算,计算后再转回小数
- 保留几位小数 比如金额,只需要精确到分即可
- 使用别人的轮子,例如:math.js
- 转成字符串相加(效率较低)